Making Addition Make Sense: How to Use an Open Number Line to Add Larger Numbers

Most of us (in the United States at least) grew up learning to add using the standard U.S. algorithm. We heard things like “carry the one,” but here’s the thing—saying “carry the one” doesn’t actually help kids understand the math they are doing. But what if there was another way to add numbers—one that is more visual, flexible, and supportive for kids? That’s where the open number line comes in.

What Is an Open Number Line?

An open number line is exactly what it sounds like—a number line without any pre-marked numbers. Instead, kids place the numbers they need to use, helping them track their thinking as they add or subtract. This strategy simultaneously draws upon AND builds a deep understanding of place value, number sense, and mental math strategies—all essential skills for success in math. 

One quick, but important note: Before using an open number line, we strongly recommend ensuring your child understands a basic number line. Our video on how to help your child get started with number lines is a great resource to check out if you or your child haven’t worked with number lines yet.

Why Is the Open Number Line So Powerful?

Unlike the standard algorithm, which often becomes a series of memorized steps, the open number line helps kids make sense of the numbers they’re working with. It allows them to:

• Use benchmark numbers (like 10s and 100s) to make adding easier

• Break numbers into parts and add in a way that makes sense to them

• See their thinking visually, reinforcing their understanding of place value

• Develop mental math strategies that support long-term success

  
  

See How an Open Number Line Works for Addition:

We walk you through two examples to see the open number line in action below BUT we encourage you to watch our YouTube video as the steps may be easier to understand in action.

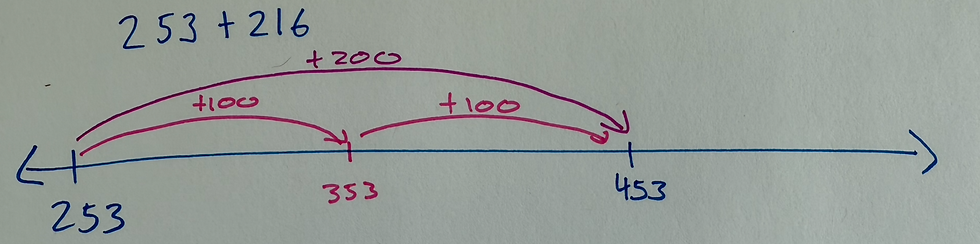
253 + 216

We start with 253 on the number line. Since addition means joining or combining numbers, we’re adding 216 to it. Instead of adding all at once, we break it down into parts:

1. Start at 253 on the Number Line

2. Add the hundreds: 253 + 200 = 453 (You could also add each 100 separately if that is more manageable for your child)

3. Add the tens: 453 + 10 = 463

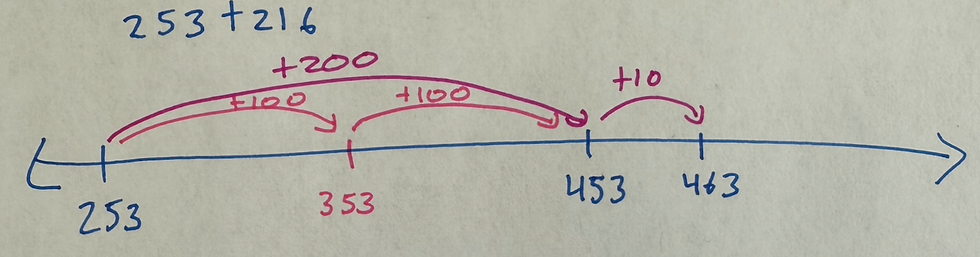
4. Add the ones: 463 + 6 = 469

   
   

   

   
   

At each step, kids can see their jumps on the number line, making it easier to follow and understand.

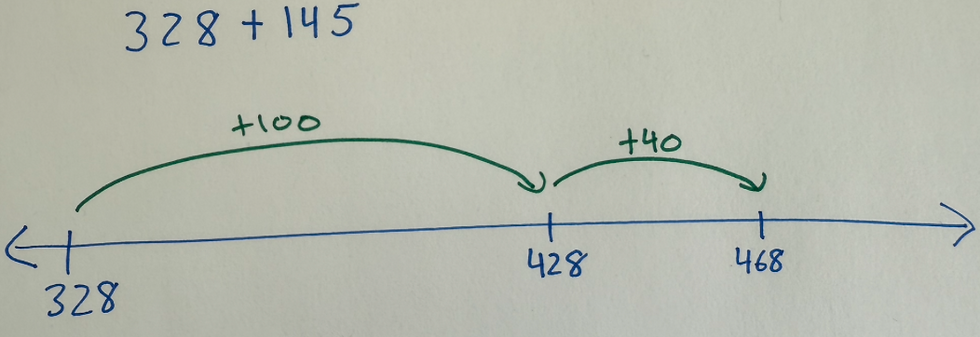
Another Example: 328 + 145

We follow the same approach:

1. Start at 328 on the number line

2. Add the hundreds: 328 + 100 = 428

   

3. Add the tens: 428 + 40 = 468

   

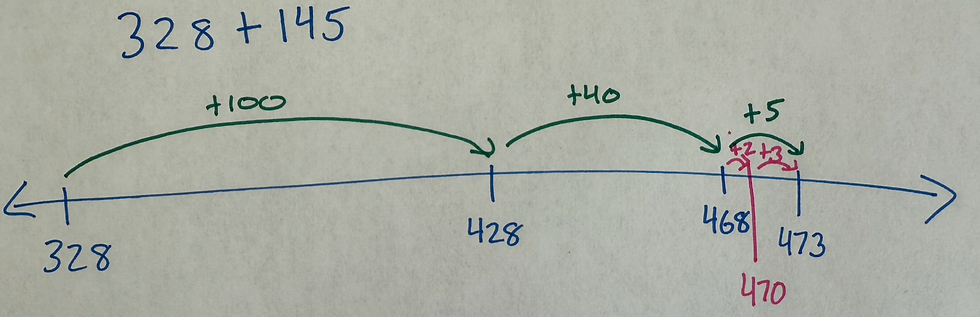
4. Add the ones: 468 + 5 = 473

It may be helpful to break the 5 apart here- adding 2 to get to 470 and then the remaining 3 to the 470 for your final total of 473

By breaking numbers apart and thinking strategically, kids develop stronger math skills that go beyond memorization.

Why This Matters for Your Child

Many kids get through early addition by memorizing steps but don’t truly understand what addition means. Using an open number line reinforces that addition is about combining amounts and lets kids explore different ways to solve problems. This flexibility builds confidence and deepens understanding, making future math concepts easier to grasp.

Try It at Home!

Want to see more examples and a step-by-step breakdown? Watch our full video on open number line addition! This method is a game-changer for helping kids with math, and the YouTube video shares even more examples to make math make sense for families.

Below are questions you might ask your child Before, During, and After working on an open number line:

Before Solving the Problem:

• What does addition mean?

• Can you explain what is happening in this problem?

• What number should we start with on the number line? Why?

• How could we break apart the other number to make adding easier?

  
  

While Working on the Open Number Line:

• What number are we at now? What should we do next?

• Can we break this number into smaller parts to make it easier to add?

• What’s a friendly number we could use to help us add?

• How did you decide where to place your jumps on the number line?

• Did we add all the parts of the second number? How do you know?

  
  

After Solving the Problem:

• How do you know your answer is correct?

• Could we add these numbers in a different way using the number line?

• How would you explain this method to someone else?